A Caveat As mentioned elsewhere, when setting out upon this expedition to Sarawak, we did not expect that these initial efforts would result in a large amount of precision data. We had never before set up our "English-style" version of the paraconical pendulum for doing experiments - indeed, it was to be our first attempt at the actual use of a paraconical pendulum at all - and we had Morley's dictum, reinforced by Allais's example, clearly in our minds: "Patience is a possession without which no one is likely to begin observations of this kind." What we hoped was that we would be able to elaborate procedures for setting up and operating the paraconical pendulum, of the type that must really be derived from experience rather than being taught second or third hand. In this aspiration we have been fully justified. We have made the first strides is learning how to do this type of experiment, and we now regard ourselves as being beyond the tyro stage. In other words, we are at the end of the beginning. Thus the most important outcomes of these experiments have been the design of the ancillary apparatus, and the formulation of the experimental procedures, described in the "Setting Up" and the "Operating" sections of this website. Any interesting numerical results, so to speak, constitute jam on the toast - they are more than we really anticipated getting when we started. Amplitude Decay Results As soon as we got the first paraconical pendulum going (the one with the lenticular brass bob), the first serious experiment we did was to measure the rate of attenuation of the amplitude of swing. Now Prof. Allais is of course quite correct to say that the decay of the amplitude is in itself not important, since there are basic theoretical reasons why the pendulum should be stopped after about fifteen minutes, and the amount of decay after fifteen minutes, with any type of bob, is not great enough to vitiate azimuth measurements. However, while one reason for using the horizontal lenticular bob is because it slips smoothly through the air and thus benefits from reduced air resistance, the rationale behind this is not so much to suffer less reduction in the amplitude of swing of the pendulum over time, but rather: (A) to minimize deflection caused by air currents from the side upon the bob, and also (B) to minimize the generation of air vortices behind the bob as it moves. It is well known that a sphere in an air current, for example, generates Karmann vortices like this: and sometimes these vortices may not be so regular as in the drawing! Naturally this kind of vortex has the potential to disturb the bob in an irregular and unpredictable manner. A vertically oriented disk-shaped bob (such as Allais used) has even more possibilities for trouble, especially in the case of a paraconical pendulum which can rotate as a whole about the axis of its rod, because if it starts moving obliquely, i.e. skewed slightly around that axis out of the plane of swing, this will generate an aerofoil effect which will cause further deviation in the same direction - like pitch instability of an aircraft wing on its own; that's why they put on horizontal stabilizers! However, with a horizontal lenticular bob these problems are almost absent, because the air slips uniformly off its sharp rear edge whatever be its orientation about the axis of the pendulum rod. A low rate of decay of the swing amplitude is the measure of this benefit. Click here to see the details of the way we found the amplitude decay for our pendulum. Precession Preliminaries First, for the benefit of the diligent who want to analyze things for themselves, we should say that a zipfile of the Excel files of all of our numerical experimental data upon which the following graphs are based, also containing the graphs themselves, may be downloaded as a zipped file by right-clicking here (it's only about 300K). Moreover, to explain the units: the precession is measured in arbitrary units established by how we printed the scales for reading the pendulum azimuth; click here to see these scales. In fact one large division corresponds to 2.048o, i.e. 0.0357 radian; and one small division (a tenth of a large division) corresponds to 12.29' of arc, i.e. 0.00357 radian. Moreover, for both of the pendulums, a positive value means an anti-clockwise precession (as seen from above, of course).
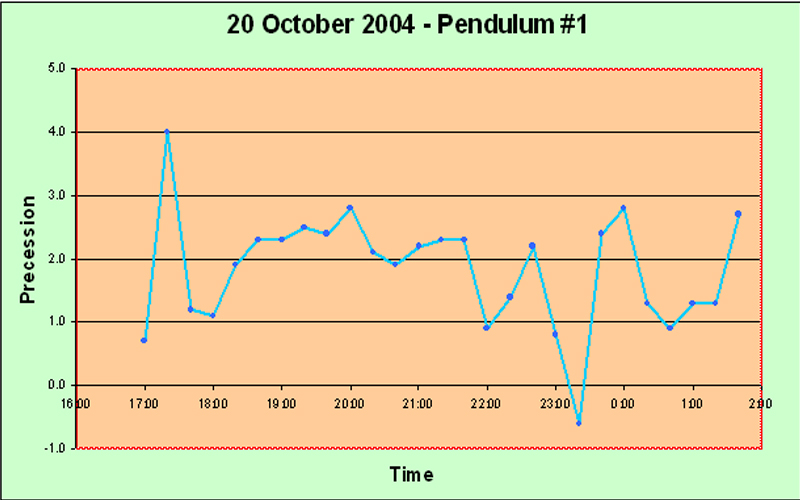
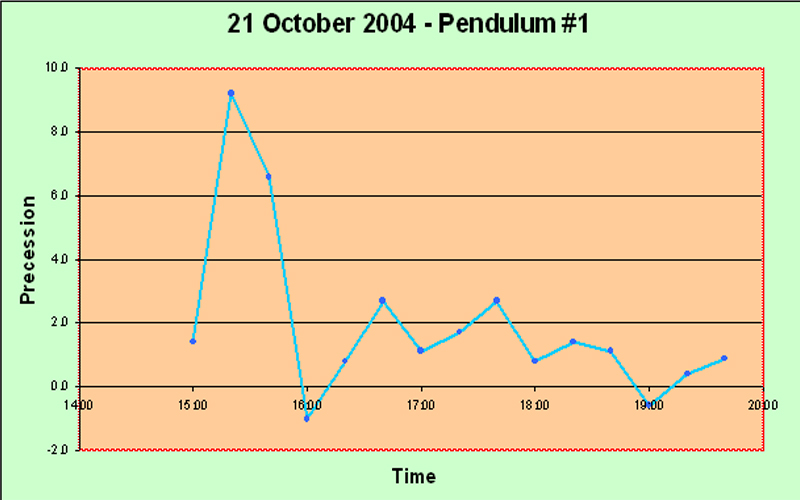
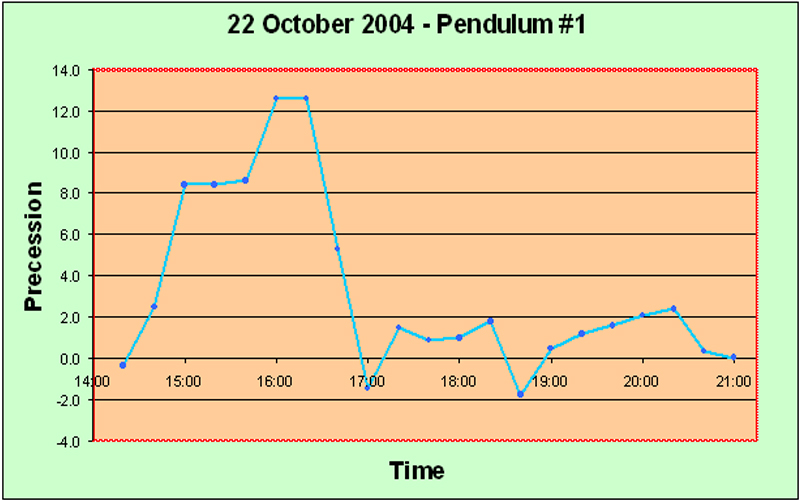
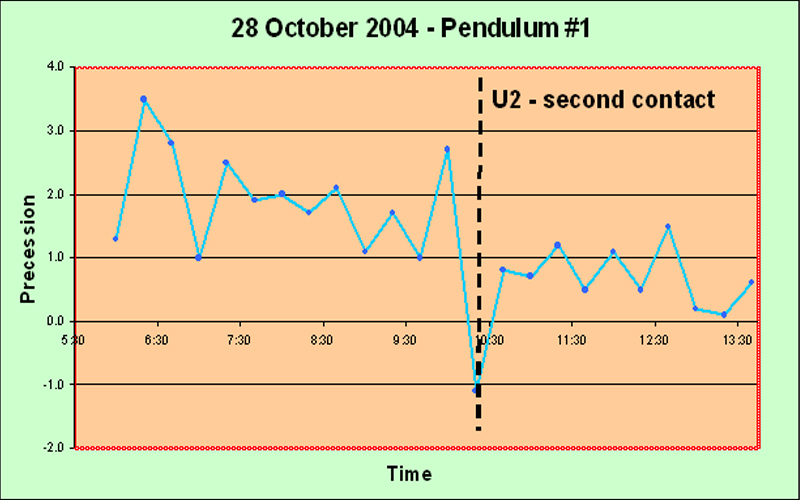
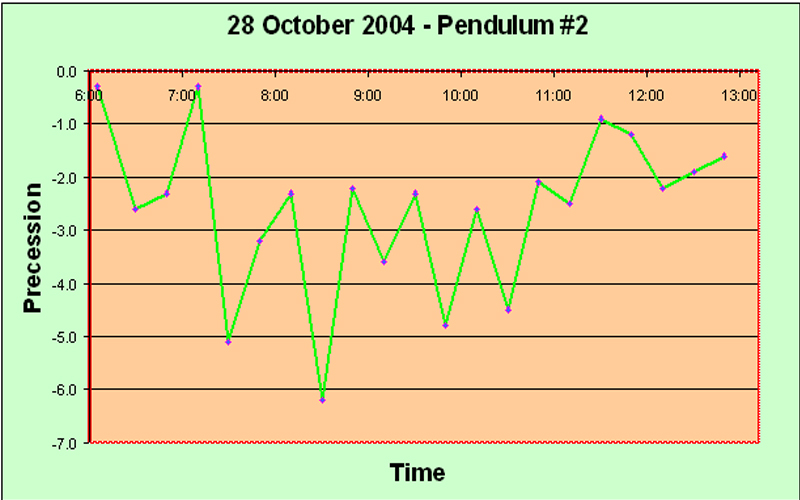
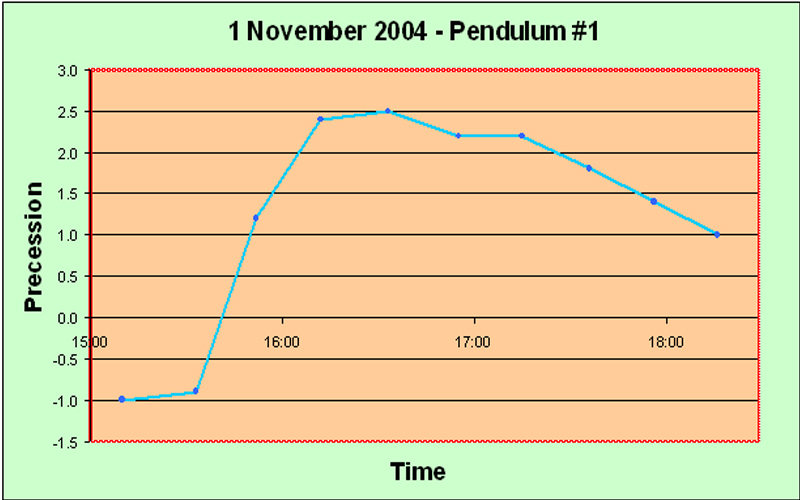
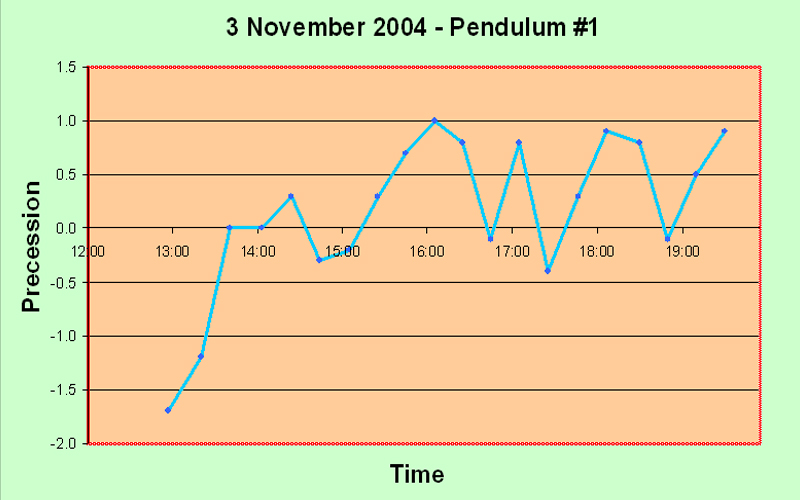
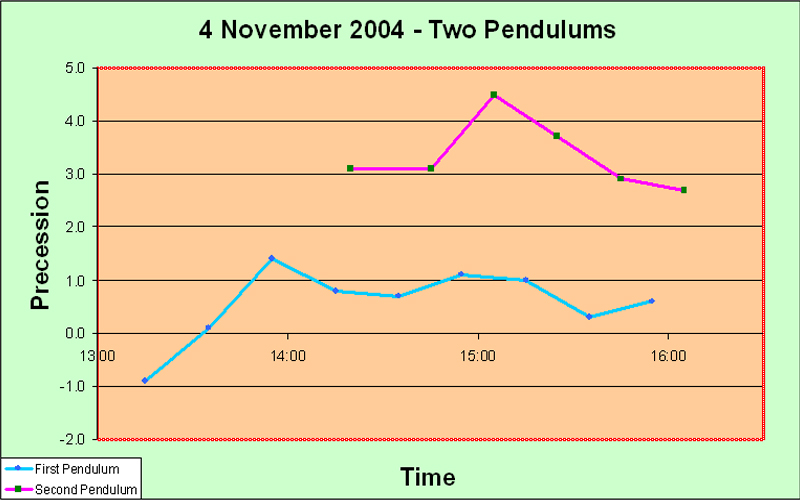
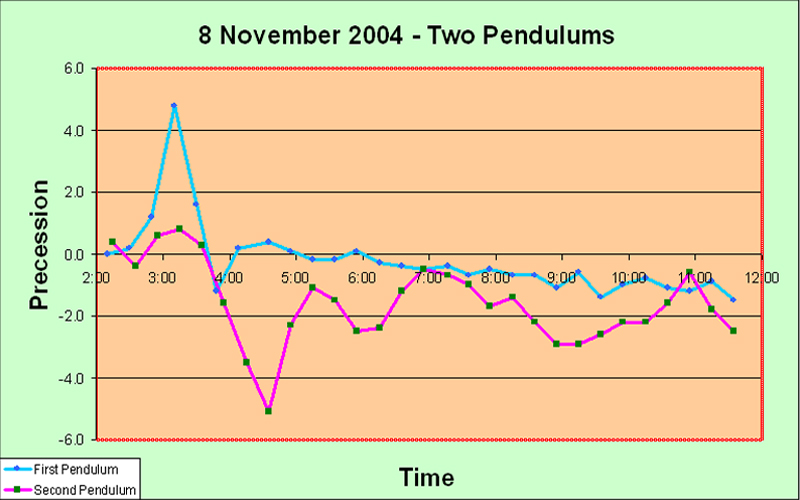
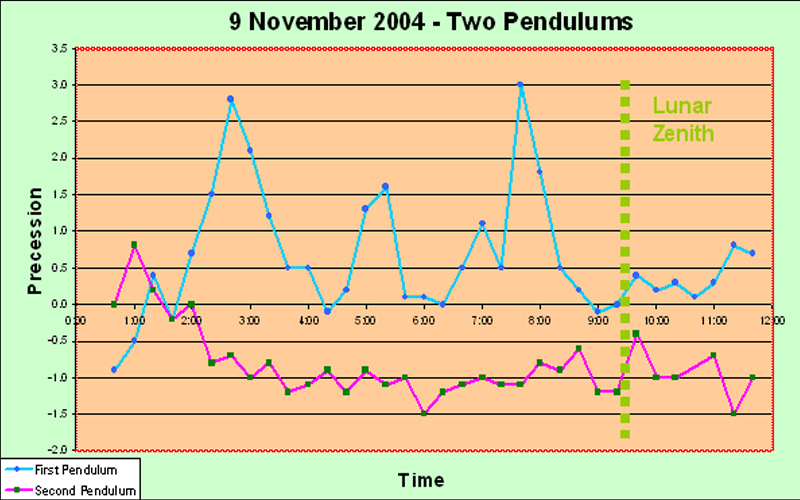
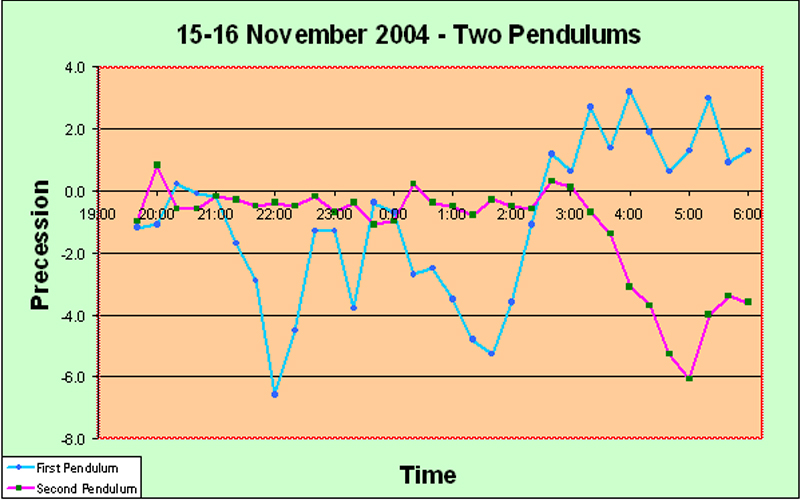
Main Precession Results It took us some time to obtain any results worth presenting. The launch procedure gave a great deal of trouble, and we consider ourselves lucky to have arrived at a reasonably satisfactory solution in the end. Another problem was that we suffered from irregularities in the motion which we believe were caused by trying for too great an amplitude of swing. Allais hypothesizes that the anomalous effects are proportional to A2/L, where A is the amplitude in radians and L is the length of the pendulum, so it is natural to try to maximize the amplitude; but we may have pushed it a bit far and encountered sporadic skidding. I advise no more than 95 mm amplitude for a seconds pendulum. In fact, quite possibly some of the random irregularities which Allais blames upon imperfections of the balls may have been due to slight skidding - he says very little about the question of amplitude, but he seems to have started off at 110 mm. And we had several debacles caused by not taking good care of the flat between runs - it is quite vulnerable to superficial rusting in the humid atmosphere of Borneo. Moreover, our handling procedure for lowering the ball and ring down onto the flat may also not have been optimal at first; we finally solved it by using the sling. Again, Allais says nothing about how he coped with this matter. But the launch procedure constituted the toughest problem. Without a purpose-built location for mounting the pendulum, it was difficult to set up a solid enough point for the launch mechanism, and we had to try many different methods. At any rate, the procedure we have explained elsewhere on this website, while not perfect, does give a launch with no visible minor axis, every time. We feel that this has been quite an accomplishment, although, as we stipulate elsewhere, "visible" is not really good enough. Airy was so right when he said "The difficulty of starting a free pendulum, so as to make it vibrate at first in a plane, is extremely great; and every experimenter ought to be prepared to judge how much of the apparent torsion of its plane of vibration is really a progression of apses due to its oval motion". We are not ashamed to repeat this quotation; it deserves to be repeated more than once. On the 14th of October, the day of the solar eclipse which passed over Anchorage, Alaska, about 7000 km from our location, we were not yet at the stage of being able to make any determinations worth showing in detail. Anecdotally we can honestly say that our pendulum appeared much more disturbed than usual, but we cannot qualify this in a scientific way. It is of interest that Professor Olenici's 3 meter long Romanian-style paraconical pendulum, in the neighboring room, also showed unusual disturbances. On the 20th of October, for the first time, we obtained quantitative results which clearly showed something objective: The first up spike may well be an error; but following that there is a long run of very consistent results, showing that the experimental procedures are reasonably consistent. And the next two down spikes and one up spike are each represented by two points, thus indicating that perhaps they are not artefacts. On 21st October, similar behavior was observed: The initial spike may be genuine; at least, it contains two data points. Subsequently the pendulum seems to calm down. Next day, on the 22nd, we obtained much more clear cut results: The big rise is obviously not caused by experimental errors, because it is very consistent over quite a few data points. That doesn't mean that it isn't caused by some systematic change due to the time of day - such as tilting of the building due to heat. But we did check the horizontality of the support flat periodically (on other days), and it didn't seem to vary much, at least within the limits of our high-precision bull's eye gauge (shown elsewhere). Note that the big rise which ended about 16:00 is completely consistent with the initial spike in the 21st October graph above. They vindicate one another. The timing of the single-data-point spike on the 20th October graph isn't far off either. Encouraged by these results, we did a really long run a few days later, on the 25th of October. This is the graph: The spike here seems to be rather later in the day - about 6 pm. Moreover, there was confused behavior in the dead hours of the night, around 3 to 4 am, unfortunately just after the start of the experiment. We were a bit concerned because all of these runs seemed to show the biggest spike near the start of the run. Perhaps there was some artefact associated with getting started... Conducting such a long series of continuous observations was quite onerous for a single observer. Came the great day: the 28th of October, the day of the lunar anti-eclipse ("anti-" meaning that the Moon was on the opposite side of the Earth from us when it went into the Earth's shadow, so we couldn't see it). On this day, the line joining the barycenters of the Sun and the Moon was scheduled to pass through the Earth within about 1000 km of our experimental location in Kuching. Although we didn't have full confidence in the apparatus as yet, we hoped to see something interesting. We had just managed to get the second pendulum working, but we were not confident of its performance. The timings of the eclipse were as follows (in local time): U1 (first contact of the Moon with the umbra) - 09:15; U2 (the Moon first becomes completely immersed in the umbra) - 10:23; maximum of eclipse - 11:03; U3 (the Moon touches the edge of the umbra on its way out) - 11:44; and U4 (the Moon passes completely out of the umbra) - 12:53. Well, the results for the first pendulum were very consistent and showed a clear trend. Obviously something objective is happening to cause this smooth downward slope, and it also exhibits a slight but steady upwards curve. There were two spikes, each represented by only a single observation, and it is interesting that one of them happened precisely at U2; but I rather doubt that they represent any real phenomenon. Apart from those spikes, the pendulum appeared much calmer than we had ever seen it before. The interesting thing is that Prof. Olenici's two pendulums in the next room also seemed extremely stable in their operation - more so than during any other experimental runs. Anecdotally, therefore, it appears that the lunar anti-eclipse effect consists of a marked absence of any perturbation - rather like Sherlock Holmes's "the strange incident of the dog in the night-time". I suppose this is really a meta-effect. At least I can confidently assert that no effect like the classical Allais Eclipse Effect occurs during an anti-lunar eclipse. For interest, we present the graph of the azimuths of our Pendulum #2 during the lunar anti-eclipse. It is clear that we hadn't got this pendulum working properly yet. The wild deviations are too much to stomach; they are capable of concealing anything. It could be argued that there is a trend towards decrease, followed by a gentle turn upwards, but I think it should be possible to get better results than this from a paraconical pendulum. For the next experimental run on 1st November we reduced the amplitude somewhat and made a few other minor modifications, and the improvement is immediately obvious: This is the kind of curve we want to see! The random fluctuations have almost disappeared, and the rise around 16:00 is very clear and consistent. We would be happy to get this kind of smooth curve for every experiment, and this ideal really ought to be attained, because there is no reason for this highly accurate pendulum to suffer any random disturbance at all, if proper experimental protocols are adhered to. It didn't last though; the next run, on 3rd November, seems to have gone bad towards the end: The rise around 16:00 is again present, and is clearly objective, but after that the pendulum seems to deviate wildly. Mind you, perhaps there really is a disturbance at a high frequency which cannot properly be shown with the integrating technique implicit in the use of a pendulum in this manner (swinging it for 15 minutes and taking the azimuthal reading). All this while we were working on the second pendulum, and on 4th November, for the first time, we got sensible-looking results with two pendulums together, albeit over only a short run: The two pendulums show clear signs of doing the same thing! humping at about 15:00. We were very encouraged, and decided to do serious overnight runs on 8th November, and also next night when the Moon passed the zenith, i.e. on the 9th. We didn't get what we expected. On the 8th of November the Moon passed the meridian about 08:30, and nothing particular happened to the pendulums. However, the first pendulum showed a large positive spike slightly after 03:00, and the second pendulum a large negative spike at 04:30. After these respective spikes, both the pendulums became basically pretty calm. Both of these spikes are clearly objective, because they both involve several data points. Why were the pendulums not behaving similarly? Well, they are of course swinging in the same starting azimuth. But they are not physically identical at all. They are in different rooms, anchored to different parts of the building which will presumably have different resilience characteristics, and different thermal flexion characteristics if that is a factor. This difference in the support characteristics was inevitable at this stage of the project. But what may be more important, is that the bobs are quite different. They are both generally disk shaped and horizontally oriented. But the first pendulum has a lenticular brass bob weighing about 12 kg, whose surface consists of two spherical caps, while the second pendulum has a mild steel bob of about 15 kg, which is disk-shaped of uniform thickness with a tapered edge. Although it might be argued that the steel is magnetic and might be affected by the Earth's magnetic field or stray fields, we do not think that this is really very important in practice. However, the vertical moment of inertia of the second bob is much greater than that of the first, probably at least double. This represents a very significant difference which could be crucial. The question of the values of the three moments of inertia of a paraconical pendulum is of the first importance. I tend to ascribe the difference in performance to this difference of vertical moment of inertia. Clearly a useful experiment would be to interchange the two pendulums between the supports and do a calibration run... Anyway, next night we did our scheduled run. Again the pendulums did different things: The second pendulum was basically quiescent this time. The first pendulum again showed a large positive spike, this time slightly before 03:00 rather than slightly after. This spike consists of five data points and therefore must be genuine. The later two spikes are also presumably genuine as well, since they each involve several readings. No particular lunar zenith effect appeared, at least not at the actual time of the zenith. Well, leaving aside for the moment the question of why the pendulums don't do the same thing, the most interesting feature of the above two graphs is this spike around 03:00 for the first pendulum. Fairly clearly it is not lunar-related, since in fact on the 9th it was a bit earlier than on the 8th, whereas the Moon's movement was (as always) about 50 minutes later, and this difference of over an hour seems too great to have been hidden by fluctuations. Therefore we decided to wait a bit (we were rather tired), and to do another run a week later, when the Moon would be at its extreme South declination and therefore as far out of the way as possible. We also decided to start earlier in the night, in order to ensure that what seemed to be the critical time of 03:00 did not fall near the beginning of the experimental run. And on the night of 15-16 November we obtained the following graph: Again the pendulums behaved quite differently - in fact, almost opposite to one another. Up till about 03:00 the first pendulum showed consistently negative precession values, with several large swings which are clearly genuine because they represent consistent trends over many readings. Meanwhile the second pendulum was very calm. At about 03:00, the first pendulum went into a strong positive trend, while the second went strongly negative slightly thereafter. The pattern after 03:00 is almost exactly the same as on 8th November. Clearly something important was happening at about 03:00... and it wasn't directly lunar-related... So what is it? Is it cosmic, or is it created internally to the experiment or its immediate environment somehow? Well, I think that thermal expansion/contraction of the building can definitely be excluded. The climate in Sarawak is uniformly warm and damp, and the air temperature does not change much. Of course the building does get much hotter during the daylight hours in the sunshine, but it has certainly cooled off completely well before midnight. Nothing much happens from midnight until dawn as far as temperature is concerned. 03:00 is about the least likely time for a sudden thermal change in the configuration of the building, that one could well imagine. Moreover, the last run of 15-16 November clearly establishes that the 03:00 spike is not an artefact caused somehow near to the start of a run. The experiment had been running for a long time before the 'witching hour' of 03:00 arrived. An electrifying (but uncertain) insight
The matter rested there for the moment. The week after, I visited Adelaide, Australia to visit with Professor Reg Cahill and his colleague Lance McCarthy at Flinders University; Cahill's websites can be accessed via this link. Both of these gentlemen are expert in the implications of C. Dayton Miller's experiments of the 1920's with his sensitive interferometer, from which Miller drew the controversial conclusion that the solar system is moving at about 200 km/sec in an approximately southwards direction (almost perpendicular to the ecliptic) through a luminiferous aether which provides a preferred frame of reference. One of the main planks in Miller's chain of reasoning was the fact that the effects which he detected showed the direction of motion to have a right ascension of 05:00 hours. This means that the velocity of absolute motion has a
maximum projection onto the plane of the interferometer at 5 hours sidereal time. Moreover, although the matter is not generally known, a fascinating series of experiments on synchronization of atomic clocks
performed in Belgium by Roland DeWitt in 1991, completely independently and in complete ignorance of Miller's work, also showed the same right ascension of 05:00 hours. It may be argued that the combination of these two discoveries ranks as the greatest scientific discovery of the 20th century... During extensive discussions with Cahill and McCarthy, I naturally brought up this question of these mysterious spikes I had seen repeatedly starting at 03:00 Malaysian time and rising. Well, said Cahill, what was that in sidereal time? We fired up a spreadsheet program he had for calculating sidereal time (right ascension); you can download it yourself by right-clicking here. And when we put in the data corresponding to 03:00 local time in Kuching: date 08/11/2004, UT 19:00 (Kuching is 8 hours ahead of UT, so the date is different), longitude 110, then, lo and behold, the corresponding sidereal time is.....05:33! It is significant that I was not personally aware of Miller and Dewitt's attribution of significance to the sidereal hour of 05:00, nor of what the sidereal time was during the experiments, nor indeed of how exactly to calculate it, until this discussion with Cahill and McCarthy. This fascinating matter rests there for the moment, as of 1 December 2004. Clearly further development of the apparatus and further observations are imperative. XXXXXX YYYYYY Back to the website main page.