The Geometry of Eclipses and Pendulums
Here's a bit of theory (mine) on the geometry of observing solar eclipses, particularly with regard to Allais-type observations using sensitive short pendulums.
Basically, there are three canonical or pure cases for eclipse observation geometry, conveniently termed "equatorial tangential", "polar", and "central". Pendulum observations on and off the eclipse track, during each of these three types of eclipse, all may be expected to investigate different components of the tensor that describes the Allais Eclipse Effect - if indeed that effect does really exist, and if in fact a tensor is the proper way to describe it...
The "equatorial tangential" case
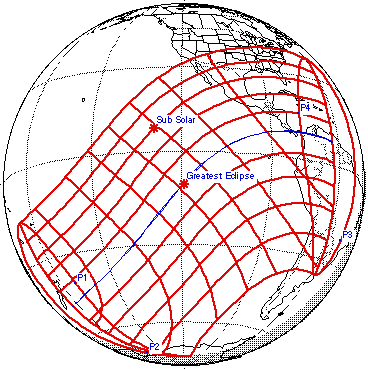
In the "equatorial tangential" case, the latitude of the observational location is low, and the overlapped sun and moon are very low in the sky and are aligned near East or West. Thus, this type of observation is performed at a tropical location, and nearly at local sunrise or sunset, thus near the beginning or the end of the eclipse track. The Sun-Moon axis drops down into the Earth, or rises up from it, through the on-track observational location.
Eclipses suitable for being observed in this manner are very common. A good example is the upcoming 8 April 2005 hybrid eclipse as viewed from Panama:

Taking cylindrical coordinates along the Sun-Moon axis, for a location upon the eclipse track (Penonome, in the case of our observations during this eclipse), near the moment of total eclipse, the eclipse axis will be moving in r, while the pendulums will be oscillating in mixtures of theta and z, and will be anomalously disturbed perpendicularly in mixtures of z and theta (if that actually happens). (For each pendulum, the nature of the mixture depends upon its azimuth of swing.)
On the other hand, for a location off to the side of the eclipse track (Bogota, for Hector Munera's observations during this eclipse), near the moment of greatest partial eclipse, the eclipse axis will be moving in theta, while the pendulums will be oscillating in mixtures of r and z and will be anomalously disturbed perpendicularly in mixtures of z and r (again, if that actually happens).
I hope that this figure, as yet not very professionally prepared, makes the matter a little clearer:
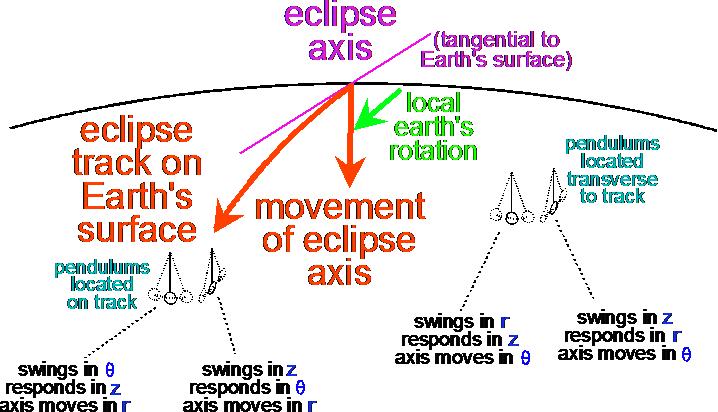
(Actually in the case of our current experiments in Central America, the movement of the eclipse axis will be upwards, out of the body of the Earth, so the straight red arrow in this figure is pointing the wrong way, but that's just a trivial difference of sign.)
The "polar" case
In the "polar" case, the latitude of the observational location is high - above the Arctic circle or below the Antarctic circle - and the overlapped sun and moon are very low in the sky and are aligned near South (or rarely North). Thus, this type of observation is performed at a polar location, and nearly at local noon (or rarely midnight-sun midnight), near the middle of the eclipse track. The Sun-Moon axis passes horizontally through the on-track observational location.
Total eclipses suitable for being observed in this manner are not very common; in fact, partial eclipses more often come quite near to this canonical case. An example is a partial eclipse on 23 October 2014 as viewed from northern Canada:
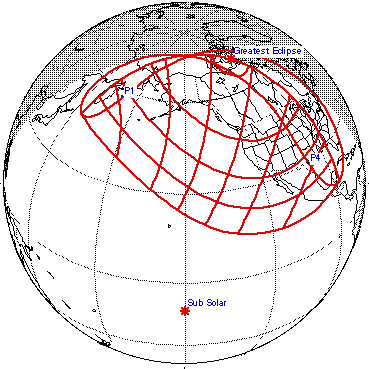
This figure illustrates this canonical polar case:
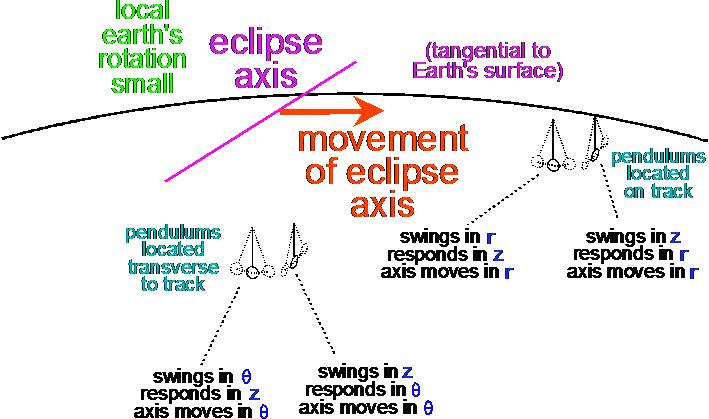
Here, for a location upon the eclipse track, near the moment of total eclipse, the eclipse axis will be moving in r, while the pendulums will be oscillating in combinations of r and z and will be anomalously disturbed perpendicularly in combinations of z and r (if that actually happens).
On the other hand, for a location off to the side of the eclipse track, near the moment of greatest partial eclipse, the eclipse axis will be moving in theta, while the pendulums will be oscillating in combinations of theta and z and will be anomalously disturbed perpendicularly in combinations of z and theta (again, if that actually happens).
The "central" case
In the canonical "central" case, the observational location is at a tropical latitude, and the overlapped sun and moon are at zenith. Thus, this type of observation is performed at local noon, near the middle of the eclipse track. The Sun-Moon axis passes vertically through the on-track observational location.
Total eclipses suitable for being observed roughly in this manner occur with moderate frequency. The most accurate case for thousands of years was the remarkable eclipse of 11 July 1991 when, at a certain point in Mexico, the Sun/Moon combination was at absolute zenith. A pretty good upcoming example is the annular eclipse of 21 June 2020 as viewed from northern India:

The following figure illustrates this canonical central case. Here, the eclipse axis runs perpendicular to the surface of the Earth, since the overlapping Sun and Moon are at the zenith. Thus, the purple line in the figure is meant to be extending perpendicularly upwards from the globe of the Earth (i.e. the figure is drawn in a sort of pseudo-perspective):
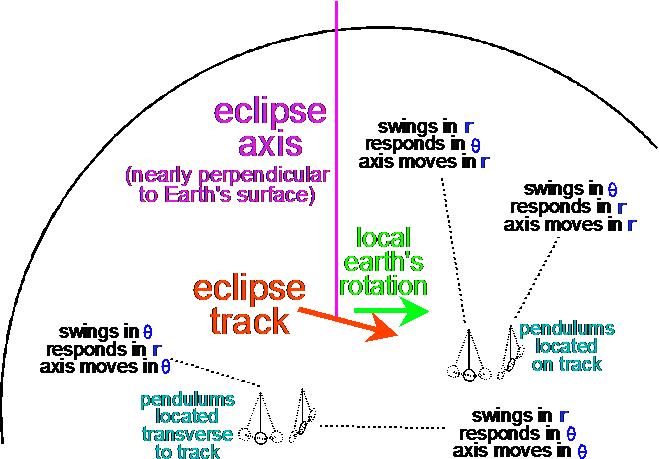
(Again, we admit that this is not a very good drawing.)
Here, for a location upon the eclipse track, near the moment of total eclipse, the eclipse axis will be moving in r, while the pendulums will be oscillating in combinations of r and theta and will be anomalously disturbed perpendicularly in combinations of theta and r (if that actually happens).
On the other hand, for a location off to the side of the eclipse track, near the moment of greatest partial eclipse, the eclipse axis will be moving in theta, while the pendulums will be oscillating in combinations of theta and r and will be anomalously disturbed perpendicularly in combinations of r and theta (again, if that actually happens).
The famous Allais observation of 1954 corresponded more closely to this central canonical case, than to either of the other two. Accordingly we consider that this case is the one most likely to yield a positive result, in terms of demonstrating a replication of the Allais Eclipse Anomaly. But we will have to wait until the eclipse of 22 September 2006 to make a good test of this central case - and then, the only suitable location will be St. Helena!
-o0o-
Thanks for the eclipse illustrations, Fred Espenak!
Back to our website main page.